题目链接：

题目大意：

已知f(0) = 1,0^0 =1,【注意，0的其他任意次方为0，虽然题没有直接给出~】，还已知f(n) = (n%10)^f(n/10),让你求f(n)%m. (2 ≤ n , m ≤ 10^9）

解题思路：

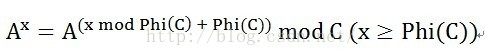
通过这个就可以递归求解。

f(n) = f(n%10)^{(f(n/10)%Phi(m)+Phi(m))}%m

递归返回值就是f(n)%m+m

注意等于0的细节部分

1 #include
     
       2 #include
      
        3 #include
       
         4 #include
        
          5 using namespace std; 6 typedef long long ll; 7 int euler_phi(int n)//求单个 8 { 9     int m = (int)sqrt(n + 0.5);10     int ans = n;11     for(int i = 2; i <= m; i++)if(n % i == 0)12     {13         ans = ans / i * (i - 1);14         while(n % i == 0)n /= i;15     }16     if(n > 1)ans = ans / n * (n - 1);17     return ans;18 }19 ll mul(ll a, ll b, ll m)20 //求a*b%m21 {22     ll ans = 0;23     a %= m;24     while(b)25     {26         if(b & 1)ans = (ans + a) % m;27         b /= 2;28         a = (a + a) % m;29     }30     return ans;31 }32 ll pow(ll a, ll b, ll m)33 {34     ll ans = 1;35     a %= m;36     while(b)37     {38         if(b & 1)ans = mul(a, ans, m);39         b /= 2;40         a = mul(a, a, m);41     }42     ans %= m;43     return ans;44 }45 ll f(ll n, ll m)46 {47     if(n < 10)return n;48     ll p = euler_phi(m);49     ll t = f(n / 10, p);50     ll ans = pow(n % 10, t, m);51     if(n % 10 == 0 && t != 0)return 0;//直接等于052     if(ans == 0)ans = m;//返回值为f(n)%m+m53     return ans;54 }55 int main()56 {57     int T;58     scanf("%d", &T);59     while(T--)60     {61         ll n, m;62         scanf("%lld%lld", &n, &m);63         printf("%lld\n", f(n, m) % m);64     }65     return 0;66 }